1. Общие представления о системе БД
2. Моделирование данных
3. Структура БД
4. Множества, домены и атрибуты
5. Представления. Таблицы и графы
6. Ограничения

return_links(); ?>

Ограничения целостности

• Определение атрибута на некотором множестве означает, что все значения должны принадлежать этому множеству. Ограничения – значения данных (Зарплата – 0..100).
• Логические ограничения – свойство, которое для данного множества истинно или ложно. Зарплата Иванова больше зарплаты Петровой.
• Обобщенные ограничения – эти ограничения относятся к множеству объектов, а не к конкретной реализации. Зарплата руководителя больше зарплаты подчиненного.

Кроме этих ограничений, называемых внешними, существуют внутренние ограничения – ограничения структуры БД.
Если атрибут это множество, то не допускается дублирование значений при вводе информации. Следовательно, нужен язык описания ограничений.
Ограничения бывают статические и динамические.
Статические определяют состояние БД.
Динамические ограничения определяют допустимые переходы БД из одного состояния в другое.

Ограничения для доменов и атрибутов

Поскольку значения атрибутов принадлежат доменам, то они наследуют свойства и ограничения этих доменов.

Чтобы изменить свойство наследования необходимо атрибуты дифференцировать. Это достигается с помощью интерпретации домена и применения техники абстракций.
Обычный путь семантизации атрибутов это применение техники абстракции.
Пусть между атрибутом и доменом, на котором он определен, существует еще один уровень абстракции.
Например:

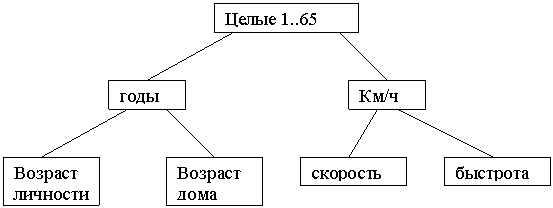
Интерпретируемые домены, то есть домены нижних уровней, ассоциируют с атрибутами единицы измерений.
Два атрибута не сравнимы, если ассоциированные с ним домены не могут быть приведены к общему ассоциированному домену.
Можно ввести не один, а несколько уровней ассоциированных доменов, для того, чтобы обеспечить точность семантического различия атрибутов.
Можно задать ограничения для любого ассоциированного домена, определив допустимые операции над доменом.
Например: возраст можно складывать и вычитать.
Можно ввести агрегатные ограничения, касающиеся всех экземпляров данного атрибута.
Например: сумма всех зарплат сотрудников не должна превышать какой-то суммы.

Ограничения на сущности и связи

В моделях данных (МД) ограничения могут быть заданы не только для атрибутов, но и для типов сущностей и типов связей.
Прежде всего, рассмотрим класс ограничений, задаваемых на отображениях между атрибутами и/или типами сущностей.
Отношение – отображение между двумя или более множествами атрибутов и оно является подмножеством их декартового произведения.
Пусть есть два множества атрибутов S1 и S2.
Эти два множества определяются как два отображения:
R: S1 -> S2 – отображение;
R1: S2 -> S1 – обратное отображение.
Множество S1 – идентификационный номер служащего, S2 – фамилия служащего.
Координальное число – число элементов множества S1 связанных с элементами множества S2.
Если в отношении имеется запись S1 (0, ?) – то это означает, что любой элемент в множестве S2 может быть связан минимум с 0 и максимум с ? элементов в S1.
Отношение S1 (0, ?), S2 (0, ?) является наиболее общим и имеет название «многие ко многим» или «M:N», то есть любой элемент множества S1 может отображаться на любое количество элементов множества S2 и наоборот. Наложив те или иные ограничения на минимальные и максимальные показатели можно получить различные типы отображений.
Например: Пусть S1 – сущность «Студент», а S2 – сущность «экзамены». Выберем отношение между этими сущностями: Сдача студентом (0, ?) экзаменов (4, 6).
Тем самым мы определили, что любой элемент множества студент должен сдать от 4 до 6 экзаменов.
Существуют различные виды ограничений на связи (отношений).
Например: R(S1(0, ?), S2(1,?)) – описывает, что каждый элемент множества S1 отображается в один или более элементов S2, но любой элемент множества S2 отображается в произвольное количество элементов множества S1.
Такое отображение называется функцией.
R(S1(0, 1), S2(0, ?)) – определяет функциональное отображение из S2 в S1, то есть любой объект в S2 отображается не более чем одним элементом из S1.
Пример: Пусть сущность «Служащий» имеет два атрибута: «номер» и «фамилия». Каждый из атрибутов определен на своем домене:
Номер -> (101, 57, 85);
Фамилия -> (Иванов, Петров, Сидоров).
Если нет ограничений, то расширением этого интенсионала, может быть следующее:

Пусть имеется ограничение: никакие служащие не имеют одинаковых номеров. Тогда расширение является недостоверным и необходимо обеспечить функциональное отображение между атрибутами «номер» и «фамилия», которое записывается в виде:
Номер => фамилия.
Это отношение называется «один к одному», то есть каждому элементу множества S1 соответствует один и только один элемент множества S2, и наоборот.
Существует еще один вид отображений «один к N» или «N к одному» – «один ко многим».
Например: служащие и отделы, в которых они работают.
Существуют полные и частичные отображения.
Частичное отображение – такое отображение, когда элемент из множества S1 отображается в 0 или более элементов множества S2, а элемент из множества S2 не более чем в один элемент множества S1, но не для всех элементов множества S2 это отображение определено.
R(S1(0, 1):S2(0, ?))
Например: каждый служащий работает не более чем в одном отделе, однако не все отделы имеют служащих.
Полное отображение – такое отображение, когда каждый элемент из множества S2 отображается точно одним элементом из множества S1, а элемент из множества S1 отображается в 0 или более элементов S2.
Например: каждый служащий должен быть закреплен за каким-либо отделом.
Существует ряд ограничений, которые нельзя выразить как ограничения на отображения.
Например: зарплата подчиненных меньше зарплаты руководителя.

Copyright © Eugene, 2007
e-mail: webmaster@ITDom.info